Table of Contents
I was very pleased to wake up the other day to find that some code I wrote for the ordered logistic distribution had been accepted into TensorFlow Probability (TFP)! However when writing this post I found that my code wasn't quite right (so my testing was bad) and I've tried to rectify that in this PR which includes the code I am using in this post.
The ordered logistic distribution is one of those annoying ones which people tend to call lots of different things and also write down differently too. The implementation I used in TFP follows Stan and PyMC3 and is currently documented here.
I've decided to show an example of all this with some soccer data, in fact the same data I used in a previous post when I diagnosed a problem with the model underestimating the draw probability. I wonder if it will be the case again when we directly consider modelling the (clipped) score difference as an ordered outcome?
I'll also implement the model in TFP and Stan and see how they compare.
For a detailed explanation on the prior used on the cutpoints and general ordinal model goodness, see this case study by Michael Betancourt.
1 Setup
Until the next TFP release (0.10.0 I think) the ordered logistic distribution will be available in the nightly TFP release, which is tested against the TensorFlow nightly release:
import tensorflow as tf import tensorflow_probability as tfp print(f"tf: {tf.__version__}") print(f"tfp: {tfp.__version__}")
tf: 2.2.0-dev20200212 tfp: 0.10.0-dev20200214
2 Data
import pandas as pd import numpy as np data_list = [] for x in range(10, 19): season = f"{x}{x+1}" url = f"http://www.football-data.co.uk/mmz4281/{season}/E0.csv" data_list.append(pd.read_csv(url)) soccer_data = ( pd.concat(data_list, axis=0) .rename( columns={ "HomeTeam": "home_team_name", "AwayTeam": "away_team_name", "FTHG": "home_goals", "FTAG": "away_goals", } ) .filter(regex="^home_|^away_") .dropna() .astype({"home_goals": np.int32, "away_goals": np.int32}) .assign( clipped_score_difference=lambda x: np.clip( x["home_goals"] - x["away_goals"], -3, 3 ) ) ) team_names = np.unique( pd.concat([soccer_data["home_team_name"], soccer_data["away_team_name"]]) ) def team_code(team_name): def fn(df): codes = pd.Categorical(df[team_name], categories=team_names).codes return codes.astype(np.int32) return fn soccer_data = soccer_data.assign( home_team=team_code("home_team_name"), away_team=team_code("away_team_name"), ) print(soccer_data.head())
home_team_name away_team_name home_goals away_goals \ 0 Aston Villa West Ham 3 0 1 Blackburn Everton 1 0 2 Bolton Fulham 0 0 3 Chelsea West Brom 6 0 4 Sunderland Birmingham 2 2 clipped_score_difference home_team away_team 0 3 1 32 1 1 3 12 2 0 5 13 3 3 10 31 4 0 27 2
3 TFP
num_outcomes = 7 num_teams = len(team_names) home_team = soccer_data["home_team"].to_numpy() away_team = soccer_data["away_team"].to_numpy() clipped_score_difference = soccer_data["clipped_score_difference"].to_numpy() tfb = tfp.bijectors tfd = tfp.distributions Root = tfd.JointDistributionCoroutine.Root def logit(x): return -tf.math.log(tf.math.reciprocal(x) - 1.0) def make_cutpoints(simplex): return logit(tf.math.cumsum(simplex[..., tf.newaxis, :-1], axis=-1)) def model(): cutpoints_simplex = yield Root(tfd.Dirichlet([2.0, 4.0, 6.0, 8.0, 6.0, 4.0, 2.0])) team_scale = yield Root(tfd.HalfNormal(1.0)) unit_team_strength = yield Root(tfd.MultivariateNormalDiag(loc=tf.zeros(num_teams))) team_strength = team_scale[..., tf.newaxis] * unit_team_strength home_strength = tf.gather(team_strength, home_team, axis=-1) away_strength = tf.gather(team_strength, away_team, axis=-1) clipped_score_difference = yield tfd.Independent( tfd.OrderedLogistic( cutpoints=make_cutpoints(cutpoints_simplex), loc=home_strength - away_strength, ), reinterpreted_batch_ndims=1, ) joint_dist = tfd.JointDistributionCoroutine(model)
What I like about TFP over stan is that it is automatic to sample from the prior (i.e. before we condition on any observed outcomes) and in this case it is obvious what the effect of our priors are. That is, how informative and realistic they are. Here I sample 1,000 datasets and consider the resulting clipped score differences:
import matplotlib.pyplot as plt plt.rcParams["figure.figsize"] = (12, 8) _, _, _, prior_predictive_samples = joint_dist.sample(1_000) sampled_score_difference_counts = [ np.bincount(sample, minlength=7) for sample in prior_predictive_samples ] observed_score_difference_counts = np.bincount(clipped_score_difference + 3) sampled_mean = np.mean(sampled_score_difference_counts, axis=0) sampled_quantiles = np.quantile( sampled_score_difference_counts, q=[0.025, 0.975], axis=0 ) low_error = sampled_mean - sampled_quantiles[0] high_error = sampled_quantiles[1] - sampled_mean plt.bar( x=np.arange(-3, 4), height=observed_score_difference_counts, label="observed data", color="blue", ) plt.errorbar( x=np.arange(-3, 4), y=sampled_mean, yerr=[low_error, high_error], fmt="o", label="simulated data", color="red", capsize=5, ) plt.legend(loc="upper left") plt.xlabel("clipped score difference") plt.ylabel("frequency")
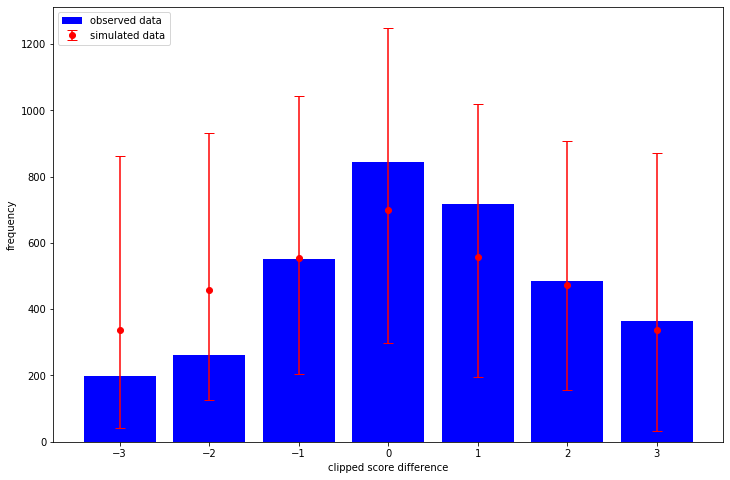
The way we have written the model is quite interpretable - so we could spend some time thinking about what priors we should choose. That's not what I'm exploring in this post however - I want to see how my posterior looks!
I'm not quite sure how to decide how many chains/samples to take with TFP on the GPU right now, adding extra chains is usually cheap though so I'm running twice as many chains (and half the number of results) compared to the stan code below. I also just totally guessed the step size, I should probably check what step sizes the warmup finds to get a feel for the typical values of them.
import time as tm num_chains = 10 num_burnin_steps = 1_000 num_results = 500 def target_log_prob_fn(*state): return joint_dist.log_prob(list(state) + [clipped_score_difference + 3]) def trace_fn(states, pkr): return ( pkr.inner_results.inner_results.target_log_prob, pkr.inner_results.inner_results.leapfrogs_taken, pkr.inner_results.inner_results.has_divergence, pkr.inner_results.inner_results.energy, pkr.inner_results.inner_results.log_accept_ratio, ) def step_size_setter_fn(pkr, new_step_size): return pkr._replace( inner_results=pkr.inner_results._replace(step_size=new_step_size) ) def step_size_getter_fn(pkr): return pkr.inner_results.step_size def log_accept_prob_getter_fn(pkr): return pkr.inner_results.log_accept_ratio initial_state = list(joint_dist.sample(num_chains)[:-1]) initial_step_size = [0.25] * len(initial_state) nuts = tfp.mcmc.NoUTurnSampler(target_log_prob_fn, step_size=initial_step_size) transformed_nuts = tfp.mcmc.TransformedTransitionKernel( inner_kernel=nuts, bijector=[tfb.SoftmaxCentered(), tfb.Softplus(), tfb.Identity()], ) adaptive_transformed_nuts = tfp.mcmc.DualAveragingStepSizeAdaptation( inner_kernel=transformed_nuts, num_adaptation_steps=int(0.8 * num_burnin_steps), target_accept_prob=0.8, step_size_setter_fn=step_size_setter_fn, step_size_getter_fn=step_size_getter_fn, log_accept_prob_getter_fn=log_accept_prob_getter_fn, ) @tf.function(autograph=False, experimental_compile=False) def run_mcmc(): return tfp.mcmc.sample_chain( num_results=num_results, current_state=initial_state, num_burnin_steps=num_burnin_steps, kernel=adaptive_transformed_nuts, trace_fn=trace_fn, )
start_tfp = tm.time() samples, sample_stats = run_mcmc() end_tfp = tm.time() print(f"TFP took {end_tfp - start_tfp:.2f} seconds")
TFP took 349.02 seconds
Was unfortunate that I couldn't get experimental_compile=True to work, which in some
examples gives a massive speed boost. It gives an error about the Gamma sampler not
being supported, which is called in the Dirichlet sampler.
As per usual I use arviz to explore the results:
import arviz as az import numpy as np sample_names = ["cutpoints_simplex", "team_scale", "unit_team_strength"] summary_vars = ["mean", "sd", "hpd_3%", "hpd_97%", "ess_bulk", "r_hat"] az_samples = { name: np.swapaxes(sample, 0, 1) for name, sample in zip(sample_names, samples) } sample_stats_names = [ "lp", "tree_size", "diverging", "energy", "mean_tree_accept", ] az_sample_stats = { name: np.swapaxes(stat, 0, 1) for name, stat in zip(sample_stats_names, sample_stats) } tfp_fit = az.from_dict( az_samples, sample_stats=az_sample_stats, coords={"teams": team_names}, dims={"unit_team_strength": ["teams"]}, ) print(az.summary(tfp_fit).filter(items=summary_vars))
mean sd hpd_3% hpd_97% ess_bulk r_hat
cutpoints_simplex[0] 0.042 0.003 0.037 0.048 4994.0 1.00
cutpoints_simplex[1] 0.064 0.004 0.057 0.072 4757.0 1.00
cutpoints_simplex[2] 0.162 0.006 0.150 0.173 5277.0 1.00
cutpoints_simplex[3] 0.283 0.008 0.268 0.299 4781.0 1.00
cutpoints_simplex[4] 0.233 0.008 0.218 0.246 5265.0 1.00
cutpoints_simplex[5] 0.134 0.006 0.123 0.145 5321.0 1.00
cutpoints_simplex[6] 0.081 0.004 0.073 0.089 9180.0 1.00
team_scale 0.616 0.081 0.473 0.771 886.0 1.01
unit_team_strength[0] 1.726 0.310 1.175 2.335 985.0 1.00
unit_team_strength[1] -0.663 0.262 -1.161 -0.173 1151.0 1.01
unit_team_strength[2] -0.341 0.445 -1.174 0.487 1761.0 1.00
unit_team_strength[3] -0.562 0.355 -1.201 0.125 1764.0 1.01
unit_team_strength[4] -0.568 0.470 -1.447 0.320 2019.0 1.00
unit_team_strength[5] -0.541 0.367 -1.237 0.132 1927.0 1.00
unit_team_strength[6] -0.320 0.288 -0.874 0.218 1483.0 1.01
unit_team_strength[7] -0.479 0.357 -1.152 0.194 1607.0 1.00
unit_team_strength[8] -0.274 0.279 -0.814 0.233 1509.0 1.00
unit_team_strength[9] -1.252 0.384 -1.997 -0.572 1383.0 1.01
unit_team_strength[10] 1.782 0.314 1.158 2.338 936.0 1.00
unit_team_strength[11] -0.025 0.252 -0.473 0.485 1230.0 1.00
unit_team_strength[12] 0.729 0.246 0.272 1.188 1002.0 1.00
unit_team_strength[13] -0.565 0.280 -1.082 -0.035 1306.0 1.00
unit_team_strength[14] -1.375 0.382 -2.064 -0.616 1391.0 1.00
unit_team_strength[15] -0.724 0.324 -1.325 -0.102 1659.0 1.00
unit_team_strength[16] 0.521 0.274 0.013 1.040 1323.0 1.00
unit_team_strength[17] 1.665 0.308 1.108 2.276 986.0 1.01
unit_team_strength[18] 2.524 0.382 1.836 3.265 905.0 1.01
unit_team_strength[19] 1.779 0.315 1.205 2.369 942.0 1.00
unit_team_strength[20] -0.616 0.448 -1.433 0.245 1766.0 1.01
unit_team_strength[21] -0.143 0.240 -0.593 0.308 1160.0 1.01
unit_team_strength[22] -0.551 0.291 -1.133 -0.043 1427.0 1.01
unit_team_strength[23] -0.759 0.317 -1.329 -0.137 1557.0 1.00
unit_team_strength[24] -0.868 0.443 -1.717 -0.048 1559.0 1.00
unit_team_strength[25] 0.293 0.251 -0.176 0.756 1190.0 1.00
unit_team_strength[26] -0.100 0.232 -0.544 0.329 1062.0 1.01
unit_team_strength[27] -0.367 0.251 -0.825 0.104 1206.0 1.01
unit_team_strength[28] -0.026 0.243 -0.474 0.436 1150.0 1.00
unit_team_strength[29] 1.482 0.291 0.921 2.018 967.0 1.00
unit_team_strength[30] -0.205 0.282 -0.740 0.333 1444.0 1.00
unit_team_strength[31] -0.191 0.232 -0.605 0.271 1080.0 1.00
unit_team_strength[32] -0.013 0.241 -0.479 0.439 1199.0 1.00
unit_team_strength[33] -0.563 0.309 -1.165 -0.013 1530.0 1.01
unit_team_strength[34] -0.538 0.328 -1.169 0.056 1612.0 1.00
az.plot_forest(tfp_fit, var_names="unit_team_strength", combined=True)

4 Stan
Note that there is a bug in the current version of pystan with the ordered logistic distribution so we need to edit some C++ code as per this PR.
data { int<lower = 1> n; int<lower = 2> num_teams; int<lower = 2> num_outcomes; int<lower = 1, upper = num_teams> home_team[n]; int<lower = 1, upper = num_teams> away_team[n]; int<lower = 1, upper = num_outcomes> clipped_score_difference[n]; } parameters { simplex[num_outcomes] cutpoints_simplex; vector[num_teams] unit_team_strength; real<lower = 0.0> team_scale; } model { vector[num_outcomes - 1] cutpoints = logit( cumulative_sum(cutpoints_simplex[1:(num_outcomes - 1)])); vector[num_teams] team_strength = team_scale * unit_team_strength; vector[n] location = team_strength[home_team] - team_strength[away_team]; cutpoints_simplex ~ dirichlet([2.0, 4.0, 6.0, 8.0, 6.0, 4.0, 2.0]'); unit_team_strength ~ std_normal(); team_scale ~ std_normal(); clipped_score_difference ~ ordered_logistic(location, cutpoints); }
import pystan import arviz as az go_faster_flags = ["-O3", "-march=native", "-ffast-math"] stan_model = pystan.StanModel( file=stan_file, model_name="ordered_model", extra_compile_args=go_faster_flags ) stan_data = { "n": len(soccer_data), "num_teams": len(team_names), "num_outcomes": 7, "home_team": soccer_data["home_team"] + 1, "away_team": soccer_data["away_team"] + 1, "clipped_score_difference": soccer_data["clipped_score_difference"] + 4, } start_stan = tm.time() stan_fit = az.from_pystan( stan_model.sampling(data=stan_data, chains=5), coords={"team": team_names}, dims={"unit_team_strength": ["team_names"]}, ) end_stan = tm.time() print(f"stan took {end_stan - start_stan:.2f} seconds")
stan took 22.13 seconds
print(az.summary(stan_fit).filter(items=summary_vars))
mean sd hpd_3% hpd_97% ess_bulk r_hat
cutpoints_simplex[0] 0.042 0.003 0.037 0.048 9153.0 1.0
cutpoints_simplex[1] 0.064 0.004 0.057 0.071 8836.0 1.0
cutpoints_simplex[2] 0.162 0.007 0.150 0.174 8737.0 1.0
cutpoints_simplex[3] 0.283 0.008 0.268 0.299 8388.0 1.0
cutpoints_simplex[4] 0.233 0.008 0.219 0.248 9650.0 1.0
cutpoints_simplex[5] 0.134 0.006 0.123 0.145 10152.0 1.0
cutpoints_simplex[6] 0.081 0.005 0.073 0.090 8664.0 1.0
unit_team_strength[0] 1.725 0.307 1.133 2.282 1015.0 1.0
unit_team_strength[1] -0.663 0.265 -1.164 -0.156 1107.0 1.0
unit_team_strength[2] -0.356 0.448 -1.170 0.499 3462.0 1.0
unit_team_strength[3] -0.564 0.365 -1.253 0.121 2398.0 1.0
unit_team_strength[4] -0.586 0.469 -1.468 0.293 3941.0 1.0
unit_team_strength[5] -0.549 0.374 -1.244 0.154 2431.0 1.0
unit_team_strength[6] -0.326 0.291 -0.901 0.182 1396.0 1.0
unit_team_strength[7] -0.477 0.350 -1.153 0.143 1982.0 1.0
unit_team_strength[8] -0.272 0.294 -0.842 0.258 1401.0 1.0
unit_team_strength[9] -1.234 0.384 -1.994 -0.550 2082.0 1.0
unit_team_strength[10] 1.781 0.310 1.194 2.353 1058.0 1.0
unit_team_strength[11] -0.019 0.261 -0.506 0.483 1102.0 1.0
unit_team_strength[12] 0.732 0.243 0.301 1.203 998.0 1.0
unit_team_strength[13] -0.565 0.279 -1.072 -0.032 1235.0 1.0
unit_team_strength[14] -1.378 0.386 -2.129 -0.655 1751.0 1.0
unit_team_strength[15] -0.722 0.328 -1.338 -0.111 1454.0 1.0
unit_team_strength[16] 0.521 0.273 0.039 1.055 1291.0 1.0
unit_team_strength[17] 1.664 0.301 1.088 2.215 1024.0 1.0
unit_team_strength[18] 2.525 0.373 1.814 3.207 1031.0 1.0
unit_team_strength[19] 1.779 0.308 1.202 2.356 1048.0 1.0
unit_team_strength[20] -0.609 0.458 -1.441 0.295 3138.0 1.0
unit_team_strength[21] -0.143 0.242 -0.615 0.295 1001.0 1.0
unit_team_strength[22] -0.550 0.293 -1.100 -0.009 1303.0 1.0
unit_team_strength[23] -0.756 0.322 -1.400 -0.184 1558.0 1.0
unit_team_strength[24] -0.859 0.449 -1.689 -0.023 3073.0 1.0
unit_team_strength[25] 0.295 0.243 -0.171 0.742 1089.0 1.0
unit_team_strength[26] -0.096 0.243 -0.525 0.387 1070.0 1.0
unit_team_strength[27] -0.366 0.252 -0.824 0.109 1067.0 1.0
unit_team_strength[28] -0.026 0.244 -0.483 0.427 1043.0 1.0
unit_team_strength[29] 1.481 0.287 0.961 2.034 995.0 1.0
unit_team_strength[30] -0.202 0.280 -0.734 0.311 1353.0 1.0
unit_team_strength[31] -0.188 0.242 -0.645 0.250 980.0 1.0
unit_team_strength[32] -0.011 0.238 -0.459 0.431 951.0 1.0
unit_team_strength[33] -0.570 0.315 -1.138 0.030 1676.0 1.0
unit_team_strength[34] -0.530 0.317 -1.089 0.091 1488.0 1.0
team_scale 0.615 0.080 0.480 0.773 1012.0 1.0
az.plot_forest(stan_fit, var_names="unit_team_strength", combined=True)

5 Posterior predictive check
Not sure how to implemenent this without copy-pasting some of the model code, would be awesome if there is a more automatic way, like when we take prior samples. Much of this code is the same as for the prior check, execpt I had to pin the sampling operation to the CPU as my (cheap) GPU would run out of memory otherwise.
cutpoints_simplex, team_scale, unit_team_strength = samples team_strength = team_scale[..., tf.newaxis] * unit_team_strength home_strength = tf.gather(team_strength, home_team, axis=-1) away_strength = tf.gather(team_strength, away_team, axis=-1) posterior_predictive_dist = tfd.OrderedLogistic( cutpoints=make_cutpoints(cutpoints_simplex), loc=home_strength - away_strength, ) with tf.device("/CPU:0"): posterior_predictive_samples = posterior_predictive_dist.sample() sampled_score_difference_counts = [ np.bincount(sample, minlength=7) for sample in tf.reshape(posterior_predictive_samples, [-1, len(soccer_data)]) ] sampled_mean = np.mean(sampled_score_difference_counts, axis=0) sampled_quantiles = np.quantile( sampled_score_difference_counts, q=[0.025, 0.975], axis=0 ) low_error = sampled_mean - sampled_quantiles[0] high_error = sampled_quantiles[1] - sampled_mean plt.bar( x=np.arange(-3, 4), height=observed_score_difference_counts, label="observed data", color="blue", ) plt.errorbar( x=np.arange(-3, 4), y=sampled_mean, yerr=[low_error, high_error], fmt="o", label="simulated data", color="red", capsize=5, ) plt.legend(loc="upper left") plt.xlabel("clipped score difference") plt.ylabel("frequency")
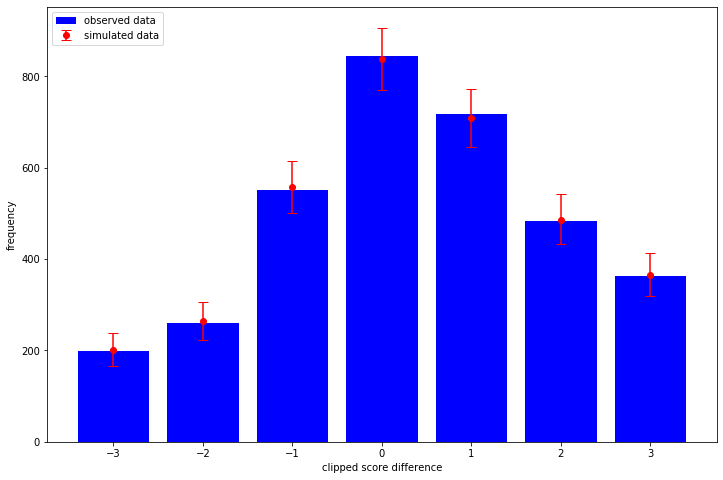
So no obvious problems with the model in this test!
6 Conclusion
I've skipped over a bunch of details in the code here, but hopefully this shows how one
might start using the new OrderedLogistic class in TFP and serves as another example
of how to run NUTS in TFP with a comparison with Stan.