This post is for experimenting. Many thanks to Carl Lieberman and Dean Attali for providing the main tools for this blog.

Here is a table with a formula for the sum:

Table 1: Witty table caption.
foo bar baz sum
1 2 3 6
42 42 41 125

Here is a reference to the above table.

Another table to check the reference is right (the taylor expansion is automatic too):

Table 2: Taylor expansions of \(\exp(x)\)
f n x Taylor expansion of order n
exp(x) 1 x 1 + x
exp(x) 2 x 1 + x + x2 / 2
exp(x) 3 x 1 + x + x2 / 2 + x3 / 6

Here is some inline latex \(\int_0^1 \omega^2 d\omega\) and then some more latex:

\begin{equation} p(\theta | D) \propto p(D | \theta) p(\theta) \end{equation}

Here is some R code I went and ran which does a plot: 

library(GGally)
ggpairs(iris)

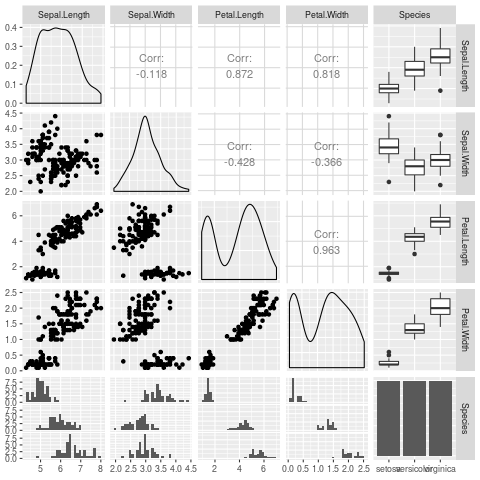
first-post-ggpairs.png

And then a reference to the R code.

Here is some C++ code: 

#include <iostream>

int main() {
    std::cout << "Hello world!";
}

Hello world!

You can also run code inline, for example the answer to 1+1 is 2.

What more could I ever need?